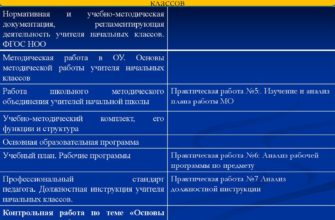
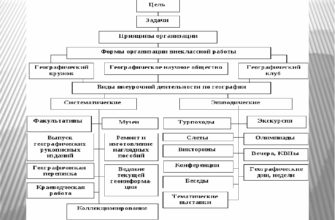
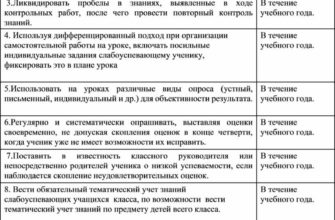
Изучение нумерации в этом пределе ведётся по тому же плану, по какому шло изучение нумерации шестизначных чисел, а именно:
3. знакомство с новыми разрядными единицами: миллион, десяток миллионов, сотня миллионов;
2) составление чисел из различных разрядных единиц и название их;
3) разложение данного числа на разрядные числа;
4) счёт тысячами и миллионами: 990 тысяч — прибавьте к этому числу 5 тысяч, к полученной сумме снова 5 тысяч и т. д. (990 тыс., 995 тыс.; 1 000 тыс., или 1 миллион; 1 миллион 5 тыс., 1 мил. 10 тыс. и т. д.); к 96 тысячам присчитывайте по одной тысяче (96 тыс., 97 тыс., 98 тыс., 99 тыс., 100 тыс., 101 тыс., 102 тыс. и т. д.);
5) составление разрядной таблицы и запоминание места каждого разряда.

6) составление таблицы классов:

7) запись и чтение многозначных чисел в пределе класса миллионов:
а) запись и чтение чисел, состоящих из круглых миллионов:
565 миллионов, 308 миллионов, 720 миллионов
565 000 000 308 000 000 720 000 000
б) запись и чтение любых девятизначных чисел со всеми значащими цифрами;
в) запись и чтение чисел с отсутствующими классами и отсутствующими единицами некоторых разрядов.
Перед тем как приступить к упражнениям в записи таких чисел, ученики повторяют следующие положения:
1. Класс объединяет 3 разряда, поэтому в каждом классе должно быть 3 цифры, но в высшем классе может быть и одна, и две цифры.
2. Иногда в числах отсутствуют единицы некоторых разрядов. Места таких разрядов должны быть заняты нулями. Если же «пустует» целый класс, то его место заполняется тремя нулями. Пример чисел с отсутствующими разрядами: 600 800 200; 504 308 705; 8 088 008; 70 060 060; 30 100 050 и т. д.
Упражнения в записи чисел сопровождаются упражнениями в чте – нии чисел с отсутствующими классами и разрядами.
Для того чтобы создать у детей правильное и более или менее конкретное представление о больших числах, нужно привести несколько примеров, характеризующих величину больших чисел, например одного миллиона. «Может ли человек прожить миллион часов? Какое расстояние займут миллион человек, если их выстроить в одну шеренгу, поставив на протяжении одного метра 2-х человек? Сколько времени потребовалось бы, чтобы записать миллион букв, если на написание одной буквы требуется одна секунда?»
Весьма желательно, чтобы учитель продемонстрировал перед учащимися лист миллиметровой бумаги размером 1 м х 1 м. На этом листе дети «увидят» миллион (миллион миллиметровых клеточек).
Показ листа и ответы на приведённые выше вопросы заставят усиленно работать детское воображение и создадут предпосылки для правильного отношения детей к величине больших чисел.
Р азло же ние ч исе л на р азр яд ные с лагае мые . Упражняясь в разложении чисел на разрядные слагаемые, ученики научатся правильно понимать значение каждой цифры числа. Задание можно давать в следующей форме: «Разложите число на разрядные слагаемые» или «Представьте данное число в виде суммы разрядных чисел». Перед тем, как приступить к записи слагаемых, анализируется состав данного числа из разрядов. Пусть дано разложить число 6 025 380. Приступая к операции разложения, ученик указывает, что данное число состоит из 6 млн. 25 тысяч 380 единиц. В классе миллионов имеются только единицы миллионов; в классе тысяч имеются десятки и единицы тысяч, в классе единиц — сотни и десятки. Значит, 6 025 380 = 6 000 000 + 20 000 + 5 000 + 300 + 80.
Не меньшее значение для понимания состава числа имеет и обратная операция: запись числа, данного в виде суммы разрядных слагаемых, по правилам нумерации. Например: 400 000 + 9 000 + 30 + 8 = 409 038.
Хорошей разновидностью упражнений этого типа являются упражнения в записи ц ифр ами таких чисел, в которых название классов записано словами, например: 60 млн. 50 тыс. = 60 050 000.
Упр ажне ние в сч ёте . Упражнение в счёте единицами целесообразно поставить в конце данной темы. Счёт единицами в пределе больших чисел громоздок и многословен; ребёнку трудно удерживать в уме большое количество слов, получаемых при счёте. Чтобы облегчить такой счёт, нужно соединить его с фиксацией чисел, с записью результатов счёта. А это возможно после того, как пройдена письменная нумерация.
Счёт единицами полезно проводить только на тех участках натурального ряда, где происходит переход из одного разряда в другой, или из одного класса в другой.
«99 997 — считайте дальше, присчитывая по единице».
«99 990 — считайте дальше, присчитывая по пятёрке, и записывайте получаемые числа».
«999 998 — считайте дальше единицами; присчитайте всего 4 единицы и записывайте получаемые числа».
Ученики считают про себя и записывают: 999 998, 999 999, 1 000 000, 1 000 001.
«Назовите число, которое на 2 единицы меньше 1 миллиона; назовите число, которое на 3 единицы меньше 100 тысяч» и т. д.
Увеличение и уменьш ение числа в 10, 100, 1 000 раз. Увеличение и уменьшение числа в 10, 100 и 1 000 раз путём приписывания и отбрасывания нулей справа помогает уяснению в десятичной нумерации принципа поместного значения цифры. Это потребуется при изучении раздробления и превращения разрядных единиц числа.
Объяснение этого вопроса проводится в следующем порядке: а) к данному числу приписывается справа один нуль; б) полученное число сравнивается с данным и устанавливается, что оно увеличилось в 10 раз;
в) выясняется, что от приписывания одного нуля число увеличивается в 10 раз потому, что после приписывания нуля каждая цифра переместилась влево на одно место; г) выводится правило: «Чтобы увеличить число в 10 раз, достаточно приписать к нему справа один нуль».
Таким же способом выясняется, что при приписывании к числу справа д вух нулей каждая цифра перемещается в л е в о на два места и получает значение в 100 раз большее; при приписывании тр ёх нулей каждая цифра перемещается влево на три места и получает значение в 1 000 раз большее.
Обратная операция — уменьшение числа в 10, 100 раз и т. д., объясняется при помощи аналогичных методических приёмов: 1) отбрасывание нулей, 2) сравнивание полученного и данного числа, 3) выяснение причины уменьшения числа и 4) вывод правила (как уменьшить число в 10, 100, 1 000 раз).
Пр е о бр аз о в ание с о став а числ а . Каждое данное число ученик должен уметь представить в различных сочетаниях его частей (например: 35 675 — это 356 сотен + 75 единиц; это 3 567 десятков + 5 единиц; это 35 тысяч + 675 единиц и т. д.). Это умение окажет ученику неоценимую услугу, когда он подойдёт к изучению умножения и деления, в особенности деления, которое невозможно без разложения делимого на его части.
Преобразование числа сводится к двум операциям — раздроблению и превращению одних разрядных чисел в другие.
Раздробление состоит в том, что данное число десятков, сотен, тысяч и т. д. выражают в единицах.
Превращение, наоборот, состоит в том, что данное число единиц преобразуют в более крупные разрядные единицы — в десятки, сотни, тысячи и т. д.
Р аздр о бл е ние . Дано 45 десятков. Раздробим это число в единицы. Сколько единиц в 45 десятках? 10 дес. — 100 единиц, 40 дес. — 400 единиц да в 5 десятках — 50 единиц, а всего 450 единиц. Значит, 45 дес. = 450.
Так же установим, что 32 сотни — 3 200; 564 сот. — 56 400.
Пр е вр ащ е ние . Дано число 700. Выразим это число в десятках, иначе говоря, узнаем, сколько десятков в 700, или в 7 сотнях? В одной сотне 10 десятков. В 7 сотнях — 70 десятков. Значит, 700 = 70 десяткам. В числе 900 — 90 десятков. Значит, чтобы узнать, сколько десятков в числе 720, отбросим нуль, получится 72. Итак, 720 = 72 дес.; 930 = 93 дес.; 6 840 = 684 дес. и т. д.
Так же покажем, что 200 — это 2 сотни; 600 — это 6 сотен; 1 500 — это 15 сотен. Значит, 3 600 = 36 сотням; 8 900 = 89 сотням; 14 600 = 146 сотням.
Но сколько десятков будет в числе, которое оканчивается не нулём, а какой-либо значащей цифрой? Например, сколько всего десятков будет в числах 75? 456? 1 238? 25 815?
Ясно, что десятков не будет только в разряде единиц. Во всех остальных разрядах десятки есть. Единицы отбрасываем, а всё остальное число и будет числом десятков. Поэтому 75 = 7 дес. + 5 ед.; 456 = 45 дес. + 6 ед.; 1 238 = 123 дес. + 8 ед.
Сколько всего сотен в числах: 638? 3 149? 63 714? Сотен нет только в единицах и десятках: они меньше сотни. А во всех других разрядах сотни есть. Поэтому, отбросив в числе его единицы и десятки, мы получим число сотен. Так: 638 составляют 6 сотен + 38 ед.; 3 649 = 36 сотен + 49 ед.; 63 714 = 637 сотен + 14 единиц.
Так же выделяются в числах все тысячи и другие разрядные единицы.
Источник:
Начальная школа. Настольная книга учителя – 1950, под редакцией проф.. М.А. Мельникова