Работа над новым материалом.
Для того чтобы выбор действия при решении задач на разностное сравнение чисел был осознан детьми, необходимо четко провести демонстрацию, подводящую к нужному выводу. Опишем различные варианты такой демонстрации. Учитель на глазах у детей отсчитывает 10 красных кубиков и прячет их в мешочек. Затем в другой мешочек кладет 8 синих кубиков. На доске запись: «кр. — 10, син. — 8». «Каких кубиков больше?» — спрашивает учитель. Дети скажут, что красных кубиков больше, чем синих, потому что 10 > 8. «Каких кубиков меньше?» (Синих, так как 8 < 10)
Подтвердив правильность ответа, учитель сообщает, что сегодня будут решаться новые задачи, в которых надо узнать, на сколько одно число больше или меньше другого, и предлагает внимательно следить за его действиями. «Я буду вынимать из мешочков кубики парами — красный и синий, красный и синий и т. д., пока не выну все синие кубики».
Учитель показывает, выставляя кубики на полочке парами: нижний — красный, на нем — синий. Выложив три-четыре такие пары, обращает внимание детей на запись на доске и спрашивает: «Не догадается ли кто-нибудь, сколько таких пар кубиков получится?» Если дети не смогут ответить на этот вопрос, то придется продолжить демонстрацию. Главное, чтобы все поняли, что из мешочка с синими кубиками вынули все кубики, т. е. 8, а из другого мешочка — столько же красных кубиков, то есть тоже 8, и в нем остались «лишние» красные кубики, которым не нашлось пары.
После этого еще раз следует спросить: «Сколько было красных кубиков? (10) Сколько их вынули?» (8), выяснить, как узнать, сколько же их осталось. (10 — 8 = 2) Формулируется ответ на вопрос задачи: красных кубиков на 2 больше чем синих. Для подведения к выводу полезно спросить еще раз каким действием узнали, на сколько 10 больше, чем 8.
Демонстрацию можно провести и с использованием фланелеграфа или магнитной доски. В этом случае сравниваемые группы предметов (например, 8 треугольников и 6 квадратов) располагают на доске так, чтобы нельзя было сразу заметить, что треугольников на 2 больше, чем квадратов. Учитель снимает пары фигур «треугольник — квадрат», пока на доске останется только 2 треугольника. Делается вывод: чтобы узнать, на сколько больше треугольников (или на сколько меньше квадратов), мы из большего числа (8) вычли меньшее (6).
Полезно аналогичную работу выполнить с использованием индивидуальных пособий. Важно, чтобы каждый раз дети наблюдали или выполняли сами практические действия, соответствующие вычитанию: убирали, отодвигали, закрывали, зачеркивали столько предметов большей группы, сколько их в меньшей. При формулировке ответа важно каждый раз указывать, на сколько больше предметов в одной группе, на столько меньше — в другой.
Для первичного закрепления следует решить задачу, данную в учебнике. При этом необходимо рассмотреть не только сюжетную иллюстрацию к задаче, но и схематический рисунок, который по ней составлен. Пусть дети объяснят, как он выполнен. (Вместо каждой лошадки нарисовали квадрат, вместо каждого верблюда — треугольник.) «Почему 3 квадрата перечеркнуты?» (Зачеркнули столько квадратов, сколько треугольников.) Обязательно должна быть объяснена и запись. Эту работу выполняют устно, а упражнение 1 разбирают и записывают на доске и в тетрадях. (Вызванный ученик выполняет сначала схематический рисунок на доске, а остальные — в тетрадях.) Затем записывается решение и кратко ответ — Ответ: на 2 карандаша.
Работа над пройденным материалом.
1. Сравнение чисел. Начать следует с упражнений на сравнение чисел в пределах 20 по месту, которое они занимают в ряду, при этом сравнивать можно не только стоящие рядом числа. Затем полезно использовать и прием поразрядного сравнения чисел (упражнение 2). Работа проводится под руководством учителя, примеры заранее записывают на доске, каждый пример обсуждают в ходе фронтальной устной работы.
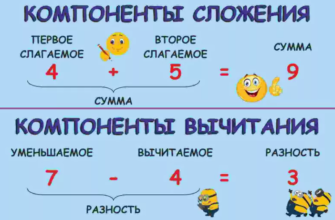
2. Использование терминов «сумма», «разность». Задания для устных вычислений можно формулировать так: «Найти сумму чисел 8 и 2, вычислить разность чисел 6 и 2».
Самостоятельно после объяснения о форме записи ученики выполняют упражнение 3.