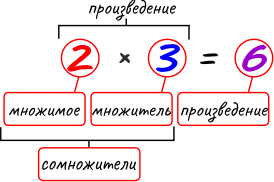
Таблица умножения может быть составлена либо по постоянному множимому, либо по постоянному множителю. Опыт российской школы подтверждает целесообразность расположения таблицы умножения по постоянному множимому, что помогает осмыслить умножение как нахождение суммы, одинаковых слагаемых.

рис. 40
Первоначально дети имеют дело с суммой двух и более одинаковых слагаемых. В этих случаях произведение всегда больше множимого. При умножении какого-либо числа на единицу нет оснований рассматривать множимое как слагаемое. Кроме того, в этих случаях произведение равно множимому. Итак, речь идет уже о некотором расширении понятия умножения. Однако по аналогии с выражением по 2 взять 2 раза, 3 раза и т. д. дети могут пользоваться выражением по 2, по 3 и т. д. взять 1 раз. В дальнейшем образные выражения заменяются отвлеченными, которые применимы к любому множителю: 3 умножить на 2; 5 умножить на 3; 4 умножить на 1 и т. д.
Умножение единицы на число не представляет никаких трудностей и вводится постепенно в процессе работы над табличными рядами. На первом уроке, посвященном умножению, рассматриваются случаи 2 x 2; 2 x 3; 2 x 4 и 2 x 5. Цель урока — ввести выражение «по 2 взять столько-то раз» и показать запись этого выражения (рис. 40). Новое выражение можно пояснить на классных счетах или при помощи прямоугольников, на каждый из которых наклеено по два кружка. Учитель берет и ставит в первом ряду на наборном полотне два таких прямоугольника, во втором ряду – три прямоугольника и т. д. Против каждого ряда он записывает под диктовку детей соответствующие суммы:
2 + 2 = 4
2 + 2 + 2 = 6 и т, д.
Составив сумму из пяти двоек, учитель подчеркивает неудобство такой длинной записи и объясняет, что ее можно заменить более короткой, которая читается так: по 2 взять 5 раз, получится 10.
Дети повторяют новое выражение, а затем сами заменяют сложение умножением. Учитель дополняет запись на доске и предлагает ученикам записать все четыре произведения в тетрадях столбиком, оставляя место для остальных случаев.
На следующем уроке можно заняться остальными случаями умножения числа 2. Однако, если иметь в виду более обстоятельное выяснение смысла умножения, что является первоочередной задачей при знакомстве с новым действием, полезно продемонстрировать процесс набирания одинаковых слагаемых на разных числах. .’ Детям предлагается взять из их индивидуальных наборов 2 раза по 3 кружка, 3 раза по 3 палочки; отсчитать 3 монеты по 5 коп.; отложить на классных счетах 2 раза по 4 косточки и т. д. Каждый раз формулируется соответствующее образное выражение и устанавливается полученный результат: по 3 кружка взять 2 раза, получится 6 кружков, по 5 коп. взять 3 раза, получится 15 коп. Результаты дети находят сложением, а затем записывают соответствующие примеры без наименований в тетрадях.
Оставшиеся случаи умножения числа 2 (на 6, 7, 8 , 9 и 10) можно пояснить на классных счетах, откладывая по две косточки на каждой проволоке сверху вниз. Дети сами формулируют новые случаи умножения и записывают их под первыми четырьмя.

рис.41
Изучая один за другим табличные ряды, дети продолжают понимать умножение как сложение одинаковых слагаемых. От набирания групп предметов можно перейти к рисованию в тетрадях кружков, палочек, крестиков, треугольников, располагая их по-разному (рис. 41).
Попутно можно предложить детям вспомнить, какие предметы считают в жизни парами (ботинки, перчатки, конверты с марками — пара на 9 коп.), десятками (яйца, пуговицы).
Чтобы подчеркнуть связь между умножением и сложением, предлагаются примеры на замену умножения сложением и наоборот: 3 х 4 = 3 + 3 + 3 + 3 и 4 х 3 = 4 + 4 + 4.
Наряду с этим выполняется обратное упражнение: 2 + 2 + 2 + 2 + 2 = 2 х 5; 3 + 3 + 3 + 3 = 3 х 4 и т. д.
Чтобы подчеркнуть существенный признак умножения — равенство слагаемых, наряду с примерами на одинаковые слагаемые даются примеры с разными слагаемыми. Дети устанавливают, что в одном случае можно заменить сложение умножением, а в другом случае нельзя этого сделать.
Постепенно выясняется существенный признак умножения и отбрасываются несущественные признаки (число слагаемых), что дает возможность ввести и такой случай, как умножение любого числа на единицу. При этом от образной формулировки умножения дети переходят к отвлеченной формулировке действия. В частности, это облегчает чтение примеров в два действия вида: (3 + 2) х 4, введение которых в программу I класса, безусловно, желательно.
Попутно с установлением связи между умножением и сложением необходимо добиться дифференциации этих действий. Различие между сложением и умножением можно показать на решении задач с одинаковыми числами:
а) В классе 3 окна, на каждом из них по 4 горшка с цветами; сколько всего горшков с цветами в этом классе?
б) На одном окне стоит 4 горшка с цветами, а на другом — 3 горшка; сколько всего горшков с цветами на этих окнах?
На доске делается запись решения обеих задач:
а) 4 г. Х 3 = 12 г.
б) 4 г. + 3 г. = 7 г.
Сравнивая эти записи, дети устанавливают, что, несмотря на одинаковые числа, ответы получились разные, так как в первом случае надо по 4 горшка взять 3 раза, во втором — к 4 горшкам прибавить 3 горшка.
В связи с этим возникает вопрос о различении множимого и множителя. В последнее время раздаются голоса (например, некоторых методистов Эстонии) за отказ от этого «обременительного» для детей и по существу ненужного различения, поскольку они легко догадываются, как решить задачу, а в дальнейшем предстоит так или иначе ввести обобщение множимого и множителя в качестве равноправных сомножителей.
Нет никаких оснований избегать некоторых трудностей, поскольку преодоление трудностей содействует умственному развитию учащихся. Да и в математике не без основания различаются термины множимое и множитель, причем отмечается особый характер множителя как оператора.
Итак, при решении задач и примеров в I классе следует различать множимое и множитель: на первом месте писать множимое, на втором — множитель.
Возникает вопрос, когда подвести учащихся к обобщению множимого и множителя и познакомить детей с переместительным законом умножения.
Это можно сделать после окончания работы над умножением на основе четкого различения множимого и множителя, иначе мы рискуем оказаться перед фактом отождествления этих понятий вместо их обобщения. Дети сами подмечают тот факт, что при умножении, как при сложении, можно переставлять числа одно на место другого. Этот факт полезно пояснить на наглядном пособии (рис. 42).

рис. 42 рис. 43
Треугольники можно рассматривать поперечно и продольно. Если их рассматривать в горизонтальном направлении, получается одна запись, а в вертикальном — другая.
Аналогичным образом поясняется переместительность умножения для следующего табличного ряда (рис. 43).
Что касается других законов умножения, то их роль в данном концентре весьма ограничена. Если и можно использовать в некоторой мере распределительный закон, то лишь по отношению к произведению 2-5, которое служит опорой для остальных случаев умножения по 2 в пределах двадцати. Сочетательный закон умножения труден даже для учеников II класса. Решая пример (3 х 2) х 3, дети думают, что умножили число 3 не на 6, а на 5, то есть рассматривают 2 и 3 не как сомножители, а как слагаемые.
Полезно предлагать детям задачи на умножение, тождественные в арифметическом отношении, но по-разному сформулированные. Например:
- Купили 3 м материи по 5 руб. за метр. Сколько израсходовали денег?
- Метр материи стоит 5 руб. Купили 3 м такой материи. Сколько израсходовали денег?
Чтобы правильно записать решение таких задач, ученик должен осмыслить роль каждого числа как компонента умножения и, несмотря на то что в первом случае в тексте задачи число 3 стоит на первом месте, а число 5 на втором, не допускать записи Зм х 5.
В итоге работы над умножением дети должны усвоить смысл этого действия как нахождения суммы одинаковых слагаемых; наряду с образным выражением овладеть отвлеченной формулировкой умножить на столько-то; научиться различать сложение и умножение, множимое и множитель; получить первоначальное представление о переместительном законе умножения (легче умножить 10 на 2, чем 2 на 10); уметь воспользоваться в отдельных случаях распределительным законом умножения (2 х 8 = 2 х 5 + 2 х 3) и, наконец, знать наизусть состав чисел второго десятка из сомножителей.
Запоминанию состава чисел из сомножителей содействует следующая игра. На руках у детей карточки с числами: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18 и 20, у каждого ученика по 4 или по 5 карточек. Учитель читает пример на умножение (3 х 2, 3 х 5 и т. д.), а ученики переворачивают соответствующую карточку с ответом. Выигрывает тот, кто раньше всех перевернет свои карточки, если после проверки выяснится, что он не допустил ошибки.
Ту же игру можно построить иначе: раздать детям карточки с примерами, а читать ответы. Так, если учитель назвал число 18, ученик может перевернуть карточки с примерами: 2 х 9, 9 х 2, 3 х 6 и 6 х 3, но не более одной на прочитанное число.
Чтобы дети не смешивали выражений «умножить на столько-то» и «увеличить на столько-то», им предлагаются такие пары примеров:
- 8 увеличить на 2. 8 умножить на 2.
- 6 умножить на 3. 6 увеличить на 3.