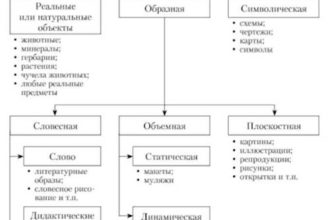
Цель наглядного обучения математике — формирование математических понятий в соответствии с особенностями детской психологии, развитие наблюдательности, воспитание внимания и памяти.
Наглядность уже давно заняла почетное место в методике обучения детей математике. Она содействует образованию ясных и точных представлений, развитию воображения, помогает от восприятия конкретного переходить к абстрактным понятиям числа, геометрической формы и т. п. «Как понятие числа, так и понятие фигуры заимствованы исключительно из внешнего мира, а не возникли в голове из чистого мышления» (Энгельс). Понятие идет за наблюдением, а потому первые математические понятия формируются на базе непосредственных восприятий и попутно создающихся представлений.
Знакомя учеников с новым понятием, следует исходить от живого созерцания конкретных ситуаций, чтобы упражнять способность детей сопоставлять и сравнивать множества, геометрические образы — углы, фигуры, тела—и устанавливать между ними сходство и различие.
Наглядное восприятие протекает не изолированно, а во взаимодействии со словом, которое усиливает значение наглядности. От правильного сочетания слова и наглядности зависит успех обучения.
Эти сочетания можно осуществлять в разной форме. Например, учитель своими вопросами направляет работу учеников. Он говорит: «отложите на своих абаках 8 кружков и прибавьте еще 5 кружков. Сколько нужно прибавить к 8 кружкам, чтобы получить 10? Сколько кружков еще осталось прибавить? Сколько всего кружков отложили на абаке? Как мы их откладывали?»
Или — по вызову учителя устные описания дают ученики. Пример. Ученики познакомились с прямоугольником и умеют перечислить его свойства. Учитель предлагает им рассмотреть квадрат и сравнить его с прямоугольником, причем он вносит поправки и дополнения там, где это нужно.
Кроме того, когда наглядные пособия дают материал для обобщения и выводов; например, при повторении свойств геометрических фигур четырехугольники даются в различных положениях, и ученики путем измерения их элементов, отвечая на вопросы учителя, устанавливают, что прямоугольники и квадраты, независимо от их расположения, сохраняют свои основные свойства.
Наглядность — одно из средств борьбы с вербализмом. Ученику легче сосредоточиться на процессе восприятия наглядного, чем на словесном изложении; даже точное словесное изложение материала учениками не всегда легко воспринимается. Осмысленность, ясность и прочность знаний зависят от умелого и своевременного использования наглядности. При этом должны затрагиваться различные органы восприятия: зрительные, речедвигательные, моторные и слуховые.
Наглядность должна содействовать координации слова и числа; по слову учителя ученик должен показывать цифры, по символу (+, :,—, X) произвести действие, по числу ударов о стол назвать число их и т. п.
Давая понятие о прямой линии, учитель прибегает к наблюдению прямых линий в классе, к отбивке прямой линии на доске или полу, к отысканию прямых линий в тетради, к получению прямых путем перегибания листа-бумаги, к ощущению скольжения пальца по ладони, по ребру линейки, наконец, к вычерчиванию и измерению отрезка прямой.
Цель этих упражнений — помочь ученику составить понятие о прямой как геометрической линии, обладающей только протяженностью. Такое использование наглядности может иметь применение при изучении не только геометрии, но и при знакомстве с основными величинами, когда за показом предмета следует измерение или взвешивание, самостоятельное изготовление наглядных пособий (модели метра, дециметра, литра) и практика измерения. Еще К. Д. Ушинский писал: «Учитель арифметики оживит свое преподавание, и может воспользоваться измерениями, чтобы самой арифметике придать наглядность, живость: следует начинать с того, чтобы познакомить детей с мерами и весами и дать им самим возможность мерить, взвешивать, считать».
Надо добиваться, чтобы ученики умели пользоваться простейшими измерительными приборами: при черчении — линейкой, циркулем, угольником; при измерениях — рулеткой или мерной веревкой, вехами и эккером. Полезно также предпослать измерениям на местности работы в классе на самодельных полигонах. При этом нужно иметь в виду, что измерительные инструменты как наглядные пособия приносят тем больше пользы, чем больше ученики с ними работают. То же нужно сказать и о структурных наглядных пособиях: счетах, абаках и т. п.
Для возбуждения интереса к математике нужно по возможности привлекать самих учеников к изготовлению наглядных пособий и дидактического материала (вырезывание, обводка, раскраска и т. п.).
Работа по изготовлению наглядных пособий расширяет пространственные представления детей, развивает их конструктивные способности и вооружает их практическими навыками.
Изготовление наглядных пособий нужно проводить преимущественно на уроках труда.
Принимая во внимание все возрастающее требование прививать ученикам навыки самостоятельной работы и шире пользоваться лабораторным методом, необходимо, чтобы у каждого ученика был па парте разнообразный дидактический материал.
Обычно учителя не останавливаются на дублировании изданных наглядных пособий (хотя и без этого пока нельзя обойтись), но нередко создают новые пособия, дополняющие и развивающие существующие стандартные пособия (счеты, абаки, цифровые кассы, счетные таблицы и др.).
В многокомплектных школах для продуктивной работы возможно кооперирование сил учителей и инструкторов труда, а также привлечение учеников старших классов. В малокомплектных школах, помимо учеников, можно привлекать к этому и родителей. Наглядность помогает также систематизировать и классифицировать изучаемые математические объекты (распределение по видам углов треугольников, иллюстрации палочками четных и нечетных чисел и т. п.).
При выборе наглядных пособий и пользовании ими учитель руководствуется психологическими и воспитательными соображениями.
Чтобы не рассеивать внимания учеников и не прививать им навыки поверхностного суждения об изучаемом вопросе, лучше ограничиваться при формировании того или иного понятия немногими, но более ценными пособиями.
Объяснения с привлечением наглядных пособий полезно дополнять разбором иллюстраций, данных в учебнике арифметики.
Наглядностью надо пользоваться тогда, когда в этом есть потребность. Не должно быть наглядности ради наглядности.
Каждому наглядному пособию следует отводить свое место в курсе начальной математики на каждой ступени изучения этого курса.