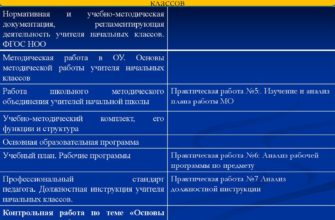
В программе по арифметике первых лет обучения элементы геометрии переплетаются с основным арифметическим материалом. Однако именно в младших классах важно установить наиболее правильные и рациональные методы ознакомления учащихся с началами геометрии и заложить в сознании детей прочный фундамент первоначальных пространственных представлений.
В 1 классе на первых же уроках необходимо проверить запас первоначальных представлений детей о величине предметов (большой — маленький, высокий — низкий, широкий — узкий и т. д.), об их относительном расположении (далеко — близко, справа — слева, в середине — с краю). Учитель может в сентябре провести с детьми ряд интересных наблюдений и игр, позволяющих выяснить запас у детей пространственных представлений. Так, во время прогулки на лужайку учитель может предложить детям собраться на её середине, а затем одним побежать вправо, а другим — влево. На той же лужайке учитель имеет все возможности проверить представления детей об относительном положении различных объектов (деревьев, кустов), а также об их относительной величине. Полезно принести в класс картину и провести беседу на тему, какие предметы видны на картине, какие из них больше, какие меньше, какие из них ближе, какие дальше.В 1 классе нужно дать детям элементарные навыки линейных измерений. В течение года дети знакомятся с метром и сантиметром и при помощи их производят измерения различных длин и расстояний. Желательно, чтобы каждый ученик сделал метр и линеечку длиной 20 — 30 см и, используя их при различных измерениях, составил правильное и точное представление о размерах метра и сантиметра. Большое значение имеет работа по уточнению глазомера учащихся. Дети по заданию учителя определяют на глаз различные длины или расстояния на местности, а затем при помощи контрольного их измерения устанавливают погрешности своего глазомера.
В деле развития пространственных представлений большое значение имеет решение таких задач, как, например: «Ширина реки зимой была 24 м. Весной во время половодья река с одной стороны вышла из берегов на 5 м, с другой стороны — на 12 м. Какой ширины была река во время половодья?»
Геометрические представления могут быть использованы при изучении чисел первого десятка. Понятие о числе формируется скорее и прочнее, если на помощь числовым представлениям детей приходят их пространственные представления. Поэтому изучение чисел первого десятка полезно иллюстрировать числовыми фигурами, используя при этом кружки, квадратики, треугольники. Например, число 5 можно иллюстрировать квадратом с пятью кружочками, число 8 — восьмью квадратиками, заключён-
ными в прямоугольник.




Таблица умножения чисел второго десятка также хорошо иллюстрируется при помощи геометрических фигур.
На этих уроках дети не только закрепляют навыки выполнения действий над числами, но попутно знакомятся с простейшими геометрическими фигурами: квадратами, треугольниками.

Во 2 классе учащиеся получают конкретное представление о длине километра. Вместе с учителем дети должны пройти по шоссе или вдоль полотна железной дороги расстояние в один километр, установить время прохождения этого пути, увид еть длину пройденного расстояния, т. е. на практике составить конкретное представление о протяжённости километра.
Во 2 классе, как и в 1, решаются задачи на развитие пространственных представлений детей.
При изучении действий над числами первой сотни и тысячи полезно применять геометрические иллюстрации. Так, таблицу умножения можно иллюстрировать геометрическими фигурами.
Интересное геометрическое изображение может получить переместительный закон умножения: «От перемены мест сомножителей произведение не меняется».
Учитель рисует на доске прямоугольник, разделённый на 12 клеточек, и предлагает учащимся сосчитать число клеточек этого прямоугольника вначале по рядам, затем по столбцам. Два результата подсчёта клеточек дети записывают: «4 х 3 = 12» и «3 х 4 = 12» и убеждаются в справедливости переместительного свойства умножения.
Понимание детьми разностного и кратного сравнения двух чисел в значительной степени облегчается, если эти сравнения сделать на прямолинейных отрезках или прямоугольных полосках.

В 3 классе дети изучают новые для них единицы измерения длины: дециметр и миллиметр. Они узнают, что в одном метре содержится 10 дециметров, изготовляют линеечки длиной в один дециметр, делят эти линеечки на сантиметры и получают конкретное представление о длине дециметра. Дети проводят практическое измерение дециметром размеров самых разнообразных предметов классной и внеклассной обстановки: длины и ширины классного стола, классного журнала, оконного стекла и т. д. Необходимо, чтобы результаты измерений ученики выражали и в метрах, и в дециметрах, и в сантиметрах, т. е. в виде составных именованных чисел. Так же учитель знакомит детей и с миллиметром. При этом ученики получают навыки аккуратного измерения небольших предметов: спичечной коробки, почтовой открытки и т. д.
В 3 классе продолжаются работы по. уточнению глазомера.
Следует предложить детям провести измерение длины своего шага в дециметрах и затем научиться определять шагами расстояния между отдельными пунктами в классе или на местности.
Дети знакомятся в 3 классе с масштабом и с вычерчиванием при его помощи определённых отрезков прямой на бумаге.
При ознакомлении с долями большое значение имеет использование геометрических представлений у детей. Допустим, что дети изучают долю «половина». Каждый получает бумажный или картонный кружок и затем по указанию учителя складывает его пополам. Каждую половину круга дети раскрашивают, в разные цвета и устанавливают, что каждая часть круга представляет его половину. Так же поступают дети и с полосками бумаги (прямоугольниками): складывают их пополам и половины раскрашивают в разные цвета. Таким же путём они знакомятся с долями V4 и У8: складывают кружки и полоски бумаги вначале пополам, а затем на четыре части (а при изучении доли1/8 на 8 частей), полученные доли фигур раскрашивают в разные цвета. Vs и 7ю доли дети изучают при помощи полос бумаги, разделённых на соответственное количество частей и раскрашенных в разные цвета.

Доли единицы возможно изучать и на кругах, начерченных на классной доске или в тетради при помощи циркуля. Эти круги делятся на определённое количество секторов в зависимости от изучаемых долей. При сгибании круга на части дети получают наглядное представление о его центре и радиусах.

Для развития пространственных представлений должно быть использовано решение задач. Особенного внимания в этом отношении заслуживают задачи на движение, решение которых должно иллюстрироваться при помощи отрезков. Допустим, что дети решают задачи на встречное движение поездов или пешеходов. В этом случае они отмечают на прямой линии два пункта А и Б, затем равными отрезками отмечают скорости их встречного движения и, наконец, условным значком место их встречи.
Заслуживают внимания, задачи на определение относительного положения и расстояний между отдельными городами. Допустим, что решается задача. «От Москвы до Курска через Тулу и Орёл 538 км. От Москвы до Орла 383 км, а от Тулы до Курска 344 км. Определить расстояние от Тулы до Орла». Дети вычерчивают схематическое расположение городов и определяют расстояние между городами.

В 3 классе имеются задачи на прямоугольные диаграммы; вычерчивание прямоугольников определённой высоты помогает детям наглядно представить соотношение между величинами задачи.
В 4 классе учащиеся переходят к изучению специальных тем по геометрии: прямая линия и отрезок, углы, прямоугольник и квадрат и их площади, куб и прямоугольный параллелепипед и их объём. Изучение должно носить сугубо практический, действенный характер. Дети наблюдают прямые линии в виде туго натянутых нитей, следа по сгибу бумаги, начерченных на классной доске и на страницах тетради прямых линий. В процессе работы они приобретают умение вычерчивать в различных направлениях и измерять отрезки прямых линий, ограниченных, например, точками А и Б. В связи с вычерчиванием прямых линий и измерением их отрезков они уясняют, что прямая линия есть кратчайшее расстояние между двумя точками, что через две точки можно провести только одну прямую линию, что две прямые линии пересекаются только в одной точке, уточняют свои представления о вертикальном и горизонтальном направлениях прямой. Одновременно с изучением основных свойств прямой линии дети упражняются в отбивании на доске, натёртой мелом, туго натянутой бечевы, в самостоятельном измерении длины и ширины классной комнаты, измерении сторон классной доски и т. д.
Измерения выполняются не только на предметах классной обстановки, но и вне класса: во дворе школы, на улице, на лужайке.
Для проведения этих измерений учитель выбирает подходящую местность и заранее составляет план проведения измерений: на сколько звеньев будут разбиты ученики, какие измерения будет выполнять каждое звено, какие нужно иметь измерительные приборы.
Остановимся на содержании одной из измерительных работ: «Провешивание прямой на местности».
Для того чтобы вовлечь в эту работу всех учащихся, класс делится на 3 — 4 звена. Каждое звено выбирает на местности две точки, между которыми необходимо провести прямую линию и измерить расстояние. Выбранные точки отмечаются шестами. Около каждого шеста располагается 2 — 3 ученика, которые составляют контрольное звено. При выполнении задания ученики этого звена наблюдают, правильно ли провешивается между шестами прямая линия, т. е. правильно ли устанавливаются по прямой линии вбиваемые между шестами вешки.

Провешивание прямой линии поручается второму звену учащихся, которые выполняют размещение между шестами вешек по прямой линии. Третье звено при помощи рулетки или землемерной цепи измеряет расстояние между шестами. Четвёртое звено записывает результаты измерений в тетради. После измерения расстояния между двумя пунктами возможно дать детям дополнительное задание: измерить это расстояние в шагах и рассчитать длину одного шага. По окончании измерения дети выполняют в тетрадях зарисовки прямолинейных отрезков, соответствующих по своей длине измеренным расстояниям на местности. При вычерчивании этих отрезков надо пользоваться определённым масштабом.
Изучение углов также должно носить опытный характер. Учитель показывает углы на предметах классной обстановки, на переплётах книг, на тетрадях. Дети вычерчивают на доске и в тетрадях прямоугольники и треугольники и отмечают их углы.

Учитель демонстрирует перед учащимися картонные модели различных углов (желательно цветные), показывая стороны и вершины углов.

На моделях углов учитель также выясняет, какие углы называются прямыми, какие — косыми. Путём наложения друг на друга цветных моделей углов учитель выясняет, что одни углы по своей величине больше прямого угла (такие углы называются тупыми углами), другие по величине меньше прямого угла (они называются острыми). Наложением друг на друга прямых углов устанавливается их равенство. Дети по заданию учителя рисуют прямые, тупые и острые углы и находят их вершины и стороны. На дом даётся задание начертить в тетрадях различные углы и заштриховать их цветными карандашами.
В дальнейшем учитель рисует на классной доске два дерева и, путём беседы, выясняет, что одно дерево изображено растущим прямо, а другое — косо.

На последующих уроках изучаются две фигуры: прямоугольник и квадрат.
Принеся в класс бумажные модели прямоугольников и квадратов, учитель раздаёт их детям и предлагает понаблюдать эти фигуры, сравнить их. Затем дети производят измерение сторон прямоугольников и квадратов и устанавливают, что у прямоугольников противоположные стороны равны между собой, а у квадратов в с е стороны равны. Путём накладывания на углы моделей наугольников ученики убеждаются, что все углы у квадратов и прямоугольников прямые, почему они и называются «прямоугольниками». Далее формулируется сходство и различие между квадратом и прямоугольником. В заключение ученики распознают прямоугольники и квадраты на предметах классной и внеклассной обстановки.
На последующем уроке ученики выполняют черчение прямоугольников и квадратов с заданными длинами сторон.
Изучение двух фигур — прямоугольника и квадрата — завершается построением прямоугольника на местности (на школьном дворе, на пришкольном участке).
Перед выходом на местность учитель знакомит детей с устройством и использованием эккера.
Класс разбивается на звенья. Допустим, что необходимо на местности наметить прямоугольник длиной 50 м и шириной — 20 м. Для этого выбирается пункт для фиксации одной вершины прямоугольника, и на этом пункте располагается первое звено учащихся с эккером в руках. Это звено составляет контрольную группу. Дети, входящие в звено, смотрят в прорези эккера и контролируют правильность размещения вешек по сторонам прямого угла. Второе звено получает в своё распоряжение вешки и, по указанию учащихся первого звена, вбивает вешки в землю так, чтобы они вытянулись по прямым линиям в направлении сторон прямого угла.
Учащиеся третьего звена при помощи рулетки отмеряют по сторонам прямого угла расстояния (в данном случае по одной стороне угла — 50 м, а по другой — 20 м).

Затем эккер переносится в другую вершину прямоугольника так, чтобы одна пара его прорезей «смотрела» на уже провешенную сторону прямого угла, третья же сторона прямоугольника провешивается в направлении другой пары прорезей.
Так на местности намечается прямоугольник заданных размеров. Эта работа требует от учащихся аккуратности, так как в случае неправильного построения прямых углов может получиться «неувязка» в нахождении четвёртой вершины прямоугольника (т. е. конечные точки первой и четвёртой сторон четырёхугольника не совпадут между собой).

Изучение темы «Измерение площади прямоугольника» ведётся по следующим этапам:
1 . Понятие о площади . Непосредственное измерение площадей прямоугольников квадратными мерами.
Учитель выясняет, что площадь — это величина поверхности фигуры. По заданию учителя дети показывают поверхность классной доски, крышки стола, переплёта книги, подоконника.
В беседе учитель напоминает классу, что отрезки измеряются линейными мерами. Подобно этому, и площади фигур измеряются путём сравнения их с какими-либо заранее выбранными площадями. Так, например, площадь крышки стола можно измерить путём накладывания на неё хотя бы одинаковых тетрадей и подсчёта их. Но тетради по своему размеру могут быть разные, и величина их площади нам неизвестна. Установлены определённые единицы измерения площадей: квадратный метр, квадратный дециметр, квадратный сантиметр. Учитель показывает образцы этих мер, сделанные из картона или бумаги. Дети рассматривают их и вычерчивают в своих тетрадях квадратный дециметр и квадратный сантиметр. Далее производится измерение площади стола и крышки парты путём укладывания на них квадратных дециметров и подсчёта их.
2 . Измерение площади прямоугольника . Учитель показывает, как можно измерить, например, площадь прямоугольной полосы длиной в 4 дм и шириной в 1 дм. В этой полосе можно уложить 4 кв. дм, причём каждый укладываемый квадратный дециметр придётся на линейный дециметр по длине. Так же показывается, что в полосе длиной в 5 дм и шириной в 1 дм укладывается 5 кв. дм и т. д

Затем измеряется площадь прямоугольника длиной в 4 дм и шириной в 2 дм. Этот прямоугольник вычерчивается на доске и разбивается на две полосы. Нижняя полоса разбивается на четыре квадрата. Дети устанавливают, что в каждой полосе прямоугольника содержится 4 кв. дм, а во всей площади прямоугольника в два раза больше, т. е. 8 кв. дм (рис. дан в уменьшенном виде).
Вычисление площади записывается так:
4 кв. дм х 2 = 8 кв. дм.
После этого дети выверчивают в своих тетрадях прямоугольники длиной в 8 см (две клеточки — один сантиметр) и шириной в 3 см и устанавливают, что в этом прямоугольнике содержится три полосы площадью по 8 кв. см каждая. Следовательно, вся площадь содержит 8 кв. см х 3 = = 24 кв. см. Так постепенно и наглядно дети подводятся к пониманию того, что длина прямоугольника всегда показывает, сколько квадратных единиц будет в одной полосе, а ширина — сколько полос содержится в прямоугольнике. Произведение количества квадратных единиц, содержащихся в одной полосе, на количество полос даст величину всей площади. Следовательно, если в длине прямоугольника 8 см, а в ширине 5 см, то его площадь будет равна 8 кв. см х 5 = 40 кв. см.
Поняв сущность процесса вычисления площади прямоугольника, дети заучивают правило: «Для того чтобы вычислить площадь прямоугольника, надо измерить в одних и тех же мерах его длину и ширину и полученные числа перемножить». Результат измерения площадей выражается всегда в квадратных единицах измерения.
После вывода правила дети применяют его к измерению площади самых разнообразных предметов: площади пола класса, крышки стола и парт, классной доски, переплёта книг и классного журнала и т. д.
При изучении мер земельных площадей на открытой местности строятся прямоугольники один площадью в один ар, другой площадью в один гектар. При этом дети размещаются по сторонам полученных на земле прямоугольников и получают конкретное представление о величине ара и гектара.
Вместе с тем на местности проводятся ещё две работы: построение прямоугольника определённой площади и измерение площади данного прямоугольного земельного участка.
Для выполнения первой работы дети делают предварительный расчёт, какой должна быть длина и ширина участка данной площади, а затем проводят практическое построение участка на местности. Для выполнения второй работы ученики делятся на три звена. Одно звено провешивает стороны прямоугольного участка, другое звено измеряет эти стороны, а третье выполняет вычислительные операции по определению величины площади участка. По возвращении в класс ученики вычерчивают планы измеренных ими участков земли.
Измерение объёма куба и прямоугольного параллелепипеда . Учащиеся знакомятся с кубом, получают модели его, наблюдают, сколько он имеет рёбер, граней, какие грани. Путём измерения рёбер куба и рассмотрения углов его граней дети убеждаются, что каждая грань куба представляет собой квадрат. Опытным путём они устанавливают, что все грани куба равны между собой.
Так же изучается и прямоугольный пар аллел епипед . Дети при помощи наблюдения и измерения устанавливают, что все боковые грани параллелепипеда представляют собой прямоугольники. Путём очерчивания граней параллелепипеда на бумаге дети убеждаются, что противоположные грани параллелепипеда равны между собой. На моделях параллелепипеда и его рисунках они показывают грани: верхнюю, нижнюю, правую, левую, переднюю и заднюю; подсчитывают количество граней, рёбер и вершин параллелепипеда; устанавливают, в чём заключается сходство и различие между кубом и параллелепипедом.
Познакомив учащихся с кубом и прямоугольным параллелепипедом, учитель переходит к измерению объёмов. Устанавливается, что предметы, имеющие форму куба или параллелепипеда, имеют вместимость. Путём пересыпания сыпучих тел, учитель показывает, как можно измерить вместимость небольшого ящика или коробки. Дети убеждаются, что вместимость тел можно измерять при помощи её сравнения с. вместимостью других тел, меньших по размеру. Учитель показывает, что вместимость ящика, коробки и других тел наиболее удобно измерять путём сравнения их с кубиками, имеющими рёбра длиной в 1 см (кубический сантиметр) или 1 дм (кубический дециметр). Сначала вместимость коробки измеряется путем её заполнения кубиками с рёбрами длиной в 1 см и подсчёта количества этих кубиков. Очень важно, чтобы было проделано несколько таких измерений при помощи кубических дециметров.

Далее учитель приносит в класс прямоугольный брус длиной, например, 8 см с сечением в один квадратный сантиметр. Этот брусок размечается на 8 кубиков, причём каждый кубик приходится на один линейный сантиметр длины и по объёму содержит один кубический сантиметр. Так дети убеждаются, что прямоугольные бруски с квадратным сечением имеют столько кубических единиц измерения, сколько линейных единиц содержится в их длине.
На том же уроке учитель показывает детям прямоугольный параллелепипед в виде слоя, у которого длина и ширина имеют по несколько сантиметров (или, что ещё более же-
лательно, дециметров), а высота содержит лишь одну единицу измерения. Допустим, что слой имеет в длину 6 см, в ширину 2 см и в высоту 1 см. Тогда этот слой распадается на два бруска, имеющих объём по 6 куб. см в каждом. Объём всего слоя: 6 куб. см * 2 = 12 куб. см.
Учитель устанавливает, что в каждом прямоугольном сло е высотой в одну единицу измерения находится столько брусков, сколько содержится в ширине слоя линейных единиц. В каждом бруске столько кубических единиц объёма, сколько содержится линейных единиц измерения по длине.
Объём слоя определяется произведением количества кубических единиц объёма одного бруска на количество брусков. Результат вычисления объёма всегда выражается в кубических единицах измерения. На уроке решают задачу: сколько кубических сантиметров уложится в коробке, если
длина ее 5 см, ширина — 4 см, высота — 1 см
» 10 см » 3 см » 1 см
» 15 см » 4 см » 1 см
В дальнейшем параллелепипед разбивается на отдельные слои, причём на каждую единицу измерений по высоте приходится слой. Пусть данный параллелепипед имеет в длину 6 см, в ширину — 3 см и в высоту — 4 см. Тогда в нём будет 4 слоя, в каждом слое по 3 бруска и в каждом бруске по 6 куб. см объёма. Общий объём всего тела будет равен 72 куб. см. Запись вычисления объёма следующая: 6 куб. см х 3 х 4 = 72 куб. см. На другом прямоугольном параллелепипеде дети ещё раз уясняют, что для нахождения объёма параллелепипеда необходимо измерить в одних и тех же единицах длину; ширину и высоту тела и результат измерения длины, выраженной в кубических единицах, умножить на ширину и высоту тела. Объём выражается только в кубических единицах.
На следующих уроках учащиеся путём самостоятельных измерений находят объёмы различных предметов окружающей обстановки (коробки, ящика, шкафа, комнаты), находят соотношение между различными кубическими единицами измерения: кубическим метром и кубическим дециметром, кубическим дециметром и кубическим сантиметром. Желательно, чтобы ученики сами склеили из картона куб с ребром в один дециметр, слепили бы из снега куб с ребром в один метр, с тем чтобы иметь конкретное представление о величине кубических мер. При вычислении объёма прямоугольного параллелепипеда дети должны хорошо уяснить, что измерение высоты тела необходимо для нахождения количества его слоев, измерение ширины — для нахождения количества брусков в каждом слое и измерение длины — для нахождения количества кубических единиц в каждом бруске. Произведение трёх измерений параллелепипеда даёт величину объёма тела, выраженную обязательно в кубических единицах.
На последующих уроках арифметики дети проводят самостоятельное измерение объёмов различных предметов классной обстановки, решают задачи на вычисление объёмов тел. Полезно сделать выход за пределы школы и выполнить измерение объёмов таких объектов, как погреб, сарай, земляной ров и т. д. Учащиеся должны выполнить измерение длины, ширины и высоты (или глубины) этих предметов, а затем произвести необходимые вычислительные операции.
Геометрический материал в начальных классах занимает небольшое количество уроков. Однако его изучение имеет большое значение для общего развития детей. Изучение геометрии развивает у учащихся интерес к самостоятельной работе, к исследованию изучаемых вопросов, стремление расширить свои знания и практические навыки. Знакомство с начальной геометрией позволяет детям в последующих классах успешно изучать географию, физику и систематический курс геометрии. Дети с большим интересом и увлечением изучают наглядную геометрию; она привлекает их конкретностью, жизненностью, наличием многих измерительных и конструктивных работ.