Вопрос об изменении результатов арифметических действий в зависимости от изменения данных имеет большое значение: он тесно связан с постепенной подготовкой детей к усвоению понятия функции, которое играет важную роль в современной математике. С понятием функциональной зависимости ученики сталкиваются с самого начала обучения арифметике, уже в I классе при изучении таблицы сложения, где сумма чисел является функцией слагаемых. На это надо обращать внимание детей, составляя с ними таблицу сложения. Так, составив таблицу прибавления единицы к числам первого десятка
1 + 1 = 2
2 + 1 = 3
3 + 1 = 4
нужно обратить внимание детей на то, что в этой таблице результаты последовательно увеличиваются на единицу (2, 3, 4 …), и поставить это увеличение в зависимость от увеличения первого слагаемого.
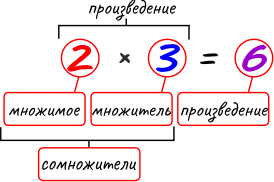
Для этой же цели должна быть использована и таблица умножения. Так, составив таблицу умножения числа 3, полезно рассмотреть с учениками, как изменяются произведения в зависимости от изменения множителя:
3 х 2= 6
3 х 3= 9
3 х 4 = 12
Сравнивая, например, произведения первой и третьей строк — 6 и 12, дети заметят, что 12 больше 6 в 2 раза. Это увеличение недопоставить в связь с увеличением в 2 раза множителя: 4 больше 2 в 2 раза.
В последующих классах хорошим материалом для иллюстрации изменения произведения в зависимости от изменения данных является зависимость площади прямоугольника от длины его сторон, объема прямоугольного параллелепипеда от длины его сторон, числового значения величины от принятой единицы измерения.
Заслуживает внимания система подготовительных упражнений, разработанная доцентом Ленинградского пединститута им. Герцена М.А. Байтовой. Эта система направлена на подготовку учеников I — III классов к усвоению изменения результатов действий в зависимости от изменения компонентов. Приведем ее здесь полностью.
В нашем опыте, — пишет М. А. Бантова, — предлагались с этой целью такие пары примеров, которые позволяют предвидеть, в котором из них ответ будет больше или меньше и на сколько больше или меньше.
Приведем несколько пар примеров для каждого класса.
В I классе уже при изучении первого десятка предлагаются детям пары примеров на сложение и вычитание, до решения которых ученик устанавливает, в котором из них ответ будет больше (меньше) и почему. Вот эти пары примеров:
4 + 3 5 + 3 8 — 2 8—5
4 + 5 2 + 3 6 — 2 8 — 3
Во II классе задания усложняются. Например, к паре примеров:
30 + 14
30 + 12
Учитель предлагает такие вопросы:
В котором примере ответ больше? Почему?
На сколько больше ответ первого примера, чем второго?
Найдите ответ первого примера.
Найдите ответ второго примера, используя ответ первого.
Аналогичные вопросы ставятся к следующим парам примеров:
37 + 18 15 + 24 40 — 8 61 — 7 70 — 12 81 — 9
42 + 18 15 + 19 42 — 8 58 — 7 70 — 8 81 — 15
Во II классе даются пары примеров на умножение. До решения этих примеров учащиеся также устанавливают, в котором примере ответ больше и на сколько больше. При этом надо исходить из определения произведения как суммы одинаковых слагаемых. Так, для пары примеров 12 х 3 надо установить, в котором из них ответ 12 х 4 больше и на сколько больше. Учитель предлагает записать каждый пример в виде суммы одинаковых слагаемых:
12 х 3 = 12 + 12 + 12;
12 х 4 = 12 + 12 + 12 + 12
Теперь легко установить, на сколько ответ второго примера больше, чем первого.
Такие же вопросы ставятся к следующим парам примеров:
8 х 6 7 х 4 15 х 4 8 х 12 14 х 3
8 х 7 7 х 6 15 х 3 7 х 12 14 х 5
В III классе предлагают пары примеров, аналогичные рассмотренным, но с многозначными числами. Кроме того, в этом классе полезно предлагать задания, обратные по отношению к рассмотренным, например:
18 + П(кв) = 40
18 + П(кв) = 48
Учитель предлагает вопросы:
- В котором примере второе слагаемое больше и почему?
- На сколько больше?
- Чему равно второе слагаемое в первом примере?
- Найдите второе слагаемое во втором примере, используя первый пример.
Такие же вопросы ставят и при решении следующих пар примеров:
П + 140 = 380 П + 390 = 600 П -60=180
П + 140 = 320 П + 480 =600 П – 60 = 240
360 – П = 80 860 – П = 580 П – 70 = 340
360 – П =120 740 – П =580 П – 90 = 340
Приведем несколько пар примеров на умножение.
356 х 8 870 х 33 86 х 15 58 х 14 81 х 12 68 х 18
356 х 9 870 х 32 87 х 15 57 х 14 81 х 14 68 х 16
35 х 3 + 35 х 7 89 х 9 + 89 95 х 99 + 95
35 х 3 + 35 х 6 89 х 10 95 х 100 – 95
63 х 15 76 х 11 32 х 17
63 х 10 + 63 х 5 76 х 12 – 76 32 х 20 – 32 х 3.
Такого рода упражнения дают учащимся хорошую подготовку к усвоению точных формулировок, в которых находит свое выражение изменение результатов действий в зависимости от изменения данных».
В старших классах начальной школы знания учеников по этому вопросу приводят в систему: им предлагают числовые примеры, они наблюдают их, изменяют числа, сравнивают данные с результатами и делают выводы.
Приведем примеры такой работы.
При изменении суммы сначала показывается, что каждая единица, прибавленная к слагаемому, входит в сумму:
15 + 5 = 20
16 + 5 = 21
После этого рассматривается изменение суммы от прибавления к слагаемому нескольких единиц, от вычитания из одного слагаемого сначала одной, потом нескольких единиц, от одновременного увеличения одного слагаемого и уменьшения другого слагаемого на одинаковое число единиц, например:
14 + 6 = 20;
12 + 8 = 20.
Каждая пара примеров подробно разбирается и после этого делаются выводы:
- Если слагаемое увеличить на несколько единиц, то и сумма увеличится, на столько же единиц.
- Если слагаемое уменьшить на несколько единиц, то и сумма уменьшится на столько же единиц.
- Если одно слагаемое увеличить, а другое уменьшить на одно и то же число, то сумма не изменится.
Эти выводы применяются на практике в устных вычислениях, когда приходится одно или оба слагаемых округлять, а также при решении задач.
После выводов учащиеся и сами составляют примеры, иллюстрирующие изменение суммы в зависимости от изменения слагаемых.
Аналогичную работу проводят и по изучению изменения разности в зависимости от изменения уменьшаемого и вычитаемого. Нужно учитывать, что характер изменения разности в зависимости от изменения вычитаемого усваивается учащимися не без труда, поэтому выводы, делаемые на основе числовых примеров, надо подкреплять фактами и примерами из жизни.
Изменение произведения рассматривают в зависимости от увеличения и уменьшения сомножителей в несколько раз. Сначала рассматривают и анализируют три пары примеров, в -которых изменяется множимое:
1) 8 х 5 = 40 2) 4 х 3 = 1.2 3) 12х.2 = 24
16 х 5 = 80 20 х 3 = 60 36 х 2 = 72
На основе рассмотрения этих примеров делается вывод:
Если множимое увеличить в несколько раз, то и произведение увеличится во столько же раз.
Дальше рассматриваются случаи изменения произведения в связи с уменьшением множимого в несколько раз:
1)10 х 4 = 40 2)12 х 6 = 72 3)24 х 2 = 48
5 х 4 = 20 4 х 6 = 24 6 х 2 = 12
На основе наблюдения и анализа этих примеров делается вывод: если множимое уменьшить в несколько раз, то и произведение уменьшится во столько же раз.
Следующий этап работы: изменение множителя, сначала увеличение, а потом уменьшение в несколько раз — и формулировка соответствующих выводов. Выводы закрепляются путем решения вопросов и задач.
Примеры вопросов:
- Множимое 20, множитель 5; найти произведение. Каково будет произведение, если множимое увеличить в 3 раза? Если множитель увеличить в 4 раза?
- Множимое увеличено в 5 раз. Что сделается с произведением? Множитель уменьшен в 2 раза. Что сделается с произведением?
Пример задачи. Два самолета вылетели с аэродрома. Один из них пролетел 1200 км. Сколько, километров пролетел за то же время другой самолет, если его скорость была вдвое больше?
При решении этой задачи учащиеся рассуждают так: сравним скорости первого и второго самолетов. Скорость второго самолета в 2 раза больше скорости первого. Значит, множимое во втором случае в 2 раза больше множимого в первом случае. А если множимое больше в 2 раза, то и произведение, или расстояние, тоже в 2 раза больше.
Вторая задача. За несколько тетрадей ученик заплатил 36 коп. Сколько денег заплатит ученик, если купит по той же цене в 3 раза больше тетрадей? В этой задаче множитель увеличен в З раза, а значит и произведение, то есть стоимость, будет в 3 раза больше.
Изменение частного рассматривается в том же плане, как и изменение произведения. Сначала изучается изменение частного в зависимости от увеличения и уменьшения делимого. Объяснение дается на задачах, а потом и на примерах.
Задача. Обыкновенный пассажирский самолет пролетел за 4 часа 1600 км. Реактивный самолет за то же время пролетел 3200 км. Во сколько раз больше километров пролетел второй самолет, чем первый, в 1 час?
1600 км : 4 = 400
3200 км : 4 = 800
Сопоставляя обе строки, ученики устанавливают, что во второй строке делимое больше в 2 раза, поэтому и частное больше в 2 раза. Изменение частного поясняется и на примерах:
1) 15: 5= 3 2) 21 : 7 =3
90 : 5 = 18 63 : 7 = 9
На основе анализа задачи и примеров делается вывод: Если делимое увеличить в несколько раз, то и частное увеличится во столько же раз.
Учащиеся сами составляют по 2 — 3 примера, подтверждающие это положение.
В таком плане рассматриваются задачи и примеры на уменьшение делимого и делается вывод: если делимое уменьшить в несколько раз, то и частное уменьшится во столько же раз.
Сложнее обстоит дело с изменением частного в зависимости от изменения делителя. На этом случае изменения следует остановиться более подробно, дать больше иллюстраций и жизненных примеров.
Для выяснения этой зависимости может служить следующая задача: Один мальчик разложил 12 карандашей в 2 коробки, другой— в 4 коробки. У которого мальчика в коробке карандашей будет меньше и во сколько раз? Решение этой задачи записывается в две строчки:
12 : 2 = 6
12 : 4 = 3
Выясняется, что делитель во втором примере увеличен в 2 раза, поэтому частное уменьшилось в 2 раза. Такая зависимость подтверждается и на других примерах и задачах.
Полезно проиллюстрировать это положение на чертеже: взять 2 равных отрезка в 12 см каждый и разделить первый отрезок на 3 части, а второй на 6 частей. Отсюда следует вывод: если делитель увеличить в несколько раз, то частное уменьшится во столько же раз.
На аналогичных примерах и задачах объясняется увеличение частного при уменьшении делителя.
Нетрудно видеть, что все эти упражнения являются прекрасным материалом для накопления у детей функциональных представлений и развития функционального мышления.